Which Register Is Used For Callee-saved?

Contents

• Registers
• Instruction format
• Aside: Directives
• Address modes
• Address computations
• %rip-relative addressing
• Arithmetic instructions
• Calling convention
• Argument passing and stack frames
• Stack
• Return accost and entry and exit sequence
• Callee-saved registers and caller-saved registers
• Base pointer (frame pointer)
• Stack size and red zone
• Branches
• Aside: C++ data structures
• Compiler optimizations

Registers

Registers are the fastest kind of memory bachelor in the machine. x86-64 has 14 full general-purpose registers and several special-purpose registers. You'll notice different naming conventions, a side effect of the long history of the x86 architecture (the 8086 was first released in 1978).

Full register (bits 0-63)	32-bit ($.25 0–31)	16-chip ($.25 0–15)	viii-flake low (bits 0–7)	eight-flake high (bits 8–15)	Use in calling convention	Callee-saved?
General-purpose registers:
%rax	%eax	%ax	%al	%ah	Return value (accumulator)	No
%rbx	%ebx	%bx	%bl	%bh	–	Yes
%rcx	%ecx	%cx	%cl	%ch	quaternary function parameter	No
%rdx	%edx	%dx	%dl	%dh	tertiary function parameter Second return register (for ix–sixteen byte return values)	No
%rsi	%esi	%si	%sil	–	2nd office parameter	No
%rdi	%edi	%di	%dil	–	1st part parameter	No
%r8	%r8d	%r8w	%r8b	–	fifth office argument	No
%r9	%r9d	%r9w	%r9b	–	6th function argument	No
%r10	%r10d	%r10w	%r10b	–	–	No
%r11	%r11d	%r11w	%r11b	–	–	No
%r12	%r12d	%r12w	%r12b	–	–	Yes
%r13	%r13d	%r13w	%r13b	–	–	Yep
%r14	%r14d	%r14w	%r14b	–	–	Yes
%r15	%r15d	%r15w	%r15b	–	–	Yes
Special-purpose registers:
%rsp	%esp	%sp	%spl	–	Stack pointer	Yeah
%rbp	%ebp	%bp	%bpl	–	Base of operations pointer (general-purpose in many compiler modes)	Yes
%rip	%eip	%ip	–	–	Pedagogy pointer (Program counter; called $pc in GDB)	*
%rflags	%eflags	%flags	–	–	Flags and condition codes	No

Unlike primary memory (which is what we think of when we discuss retentivity in a C/C++ program), registers take no addresses. At that place is no accost value that, if bandage to a arrow and dereferenced, would return the contents of the %rax register. Registers alive in a separate world from principal memory.

The %rbp annals has a special purpose: it points to the bottom of the current function'south stack frame, and local variables are frequently accessed relative to its value. Withal, when optimization is on, the compiler may determine that all local variables can exist stored in registers. This frees up %rbp for employ as some other full general-purpose register.

The relationship between dissimilar register chip widths is a petty weird.

1. Modifying a 32-scrap register proper name sets the upper 32 bits of the register to zero. Thus, later on movl $-1, %eax, the %rax annals has value 0x0000'0000'FFFF'FFFF. The aforementioned is true afterward movq $-one, %rax; addl $0, %eax! (The movq sets %rax to 0xFFFF'FFFF'FFFF'FFFF; the addl sets its upper 32 bits to zero.)

2. Modifying a 16- or viii-bit annals name leaves all other bits of the register unchanged.

There are special instructions for loading signed and unsigned 8-, sixteen-, and 32-bit quantities into registers, recognizable by instruction suffixes. For example, movzbl moves an 8-fleck quantity (a byte) into a 32-chip register (a longword) with zero extension; movslq moves a 32-bit quantity (fiftyongword) into a 64-bit register (quadword) with sign extension. There'due south no need for movzlq (why?).

Instruction format

The basic kinds of assembly instructions are:

1. Arithmetics. These instructions perform computation on values, typically values stored in registers. Nearly have zero or i source operands and 1 source/destination operand. The source operand is listed first in the educational activity, simply the source/destination operand comes first in the computation (this matters for non-commutative operators like subtraction). For case, the teaching addq %rax, %rbx performs the ciphering %rbx := %rbx + %rax.

2. Data motion. These instructions move data between registers and retention. About all have i source operand and one destination operand; the source operand comes kickoff.

3. Control flow. Normally the CPU executes instructions in sequence. Command flow instructions alter the pedagogy pointer in other ways. There are unconditional branches (the pedagogy pointer is set to a new value), conditional branches (the didactics pointer is set to a new value if a condition is true), and part telephone call and return instructions.

(We use the "AT&T syntax" for x86-64 assembly. For the "Intel syntax," which you tin can detect in online documentation from Intel, run into the Aside in CS:APP3e §3.3, p177, or Wikipedia, or other online resources. AT&T syntax is distinguished by several features, but peculiarly by the apply of percent signs for registers. Unlike AT&T syntax, Intel syntax puts destination registers earlier source registers.)

Some instructions appear to combine arithmetic and data movement. For instance, given the C code int* ip; ... ++(*ip); the compiler might generate incl (%rax) rather than movl (%rax), %ebx; incl %ebx; movl %ebx, (%rax). However, the processor actually divides these complex instructions into tiny, simpler, invisible instructions chosen microcode, because the simpler instructions can be made to execute faster. The complex incl instruction actually runs in iii phases: data movement, and so arithmetic, then information movement. This matters when nosotros introduce parallelism.

Directives

Assembly generated by a compiler contains instructions as well as labels and directives. Labels look like labelname: or labelnumber:; directives await like .directivename arguments. Labels are markers in the generated assembly, used to compute addresses. We usually see them used in control flow instructions, as in jmp L3 ("leap to L3"). Directives are instructions to the assembler; for instance, the .globl L didactics says "label L is globally visible in the executable", .align sets the alignment of the following data, .long puts a number in the output, and .text and .data define the electric current segment.

We besides frequently look at assembly that is disassembled from executable instructions by GDB, objdump -d, or objdump -S. This output looks different from compiler-generated assembly: in disassembled instructions, there are no intermediate labels or directives. This is because the labels and directives disappear during the procedure of generating executable instructions.

For example, here is some compiler-generated assembly:

                          .globl              _Z1fiii              .type              _Z1fiii,              @function              _Z1fiii:              .LFB0:              cmpl              %edx,              %esi              je              .L3              movl              %esi,              %eax              ret              .L3:              movl              %edi,              %eax              ret              .LFE0:              .size              _Z1fiii,              .-_Z1fiii                      

And a disassembly of the same part, from an object file:

                          0000000000000000              <              _Z1fiii              >:              0:              39              d6              cmp              %edx,%esi              two:              74              03              je              7              <_Z1fiii+0x7>              4:              89              f0              mov              %esi,%eax              6:              c3              retq              7:              89              f8              mov              %edi,%eax              ix:              c3              retq                      

Everything but the instructions is removed, and the helpful .L3 label has been replaced with an actual address. The function appears to be located at accost 0. This is just a placeholder; the final address is assigned by the linking process, when a last executable is created.

Finally, here is some disassembly from an executable:

                          0000000000400517              <              _Z1fiii              >:              400517:              39              d6              cmp              %edx,%esi              400519:              74              03              je              40051e              <_Z1fiii+0x7>              40051              b:              89              f0              mov              %esi,%eax              40051              d:              c3              retq              40051              eastward:              89              f8              mov              %edi,%eax              400520:              c3              retq                      

The instructions are the aforementioned, but the addresses are different. (Other compiler flags would generate different addresses.)

Address modes

Most educational activity operands use the following syntax for values. (Encounter too CS:APP3e Figure 3.iii in §3.4.i, p181.)

Type	Instance syntax	Value used
Register	%rbp	Contents of %rbp
Immediate	$0x4	0x4
Memory	0x4	Value stored at accost 0x4
	symbol_name	Value stored in global symbol_name (the compiler resolves the symbol proper name to an accost when creating the executable)
	symbol_name(%rip)	%rip-relative addressing for global
	symbol_name+4(%rip)	Simple arithmetic on symbols are immune (the compiler resolves the arithmetic when creating the executable)
	(%rax)	Value stored at address in %rax
	0x4(%rax)	Value stored at accost %rax + 4
	(%rax,%rbx)	Value stored at accost %rax + %rbx
	(%rax,%rbx,4)	Value stored at address %rax + %rbx*four
	0x18(%rax,%rbx,4)	Value stored at accost %rax + 0x18 + %rbx*4

The full form of a memory operand is offset(base of operations,index,scale), which refers to the address offset + base + index*scale. In 0x18(%rax,%rbx,4), %rax is the base, 0x18 the start, %rbx the index, and 4 the scale. The kickoff (if used) must be a constant and the base of operations and alphabetize (if used) must exist registers; the scale must be either ane, 2, 4, or 8. The default offset, base, and index are 0, and the default calibration is 1.

symbol_names are plant only in compiler-generated assembly; disassembly uses raw addresses (0x601030) or %rip-relative offsets (0x200bf2(%rip)).

Jumps and function call instructions use unlike syntax 🤷🏽‍♀️: * represents indirection.

Type	Example syntax	Address used for target of jump
Register	*%rax	Contents of %rax
Immediate	.L3	Address of .L3 (compiler-generated assembly)
	400410 or 0x400410	Given address
Retentivity	*0x200b96(%rip)	Value stored at address %rip + 0x200b96
	*(%r12,%rbp,eight)	Other address modes accepted

Address arithmetic

The base(kickoff,index,calibration) grade compactly expresses many assortment-style address computations. It'due south typically used with a mov-type instruction to dereference memory. However, the compiler can employ that form to compute addresses, thanks to the lea (Load Effective Accost) instruction.

For instance, in movl 0x18(%rax,%rbx,4), %ecx, the address %rax + 0x18 + %rbx*4 is computed, then immediately dereferenced: the 4-byte value located there is loaded into %ecx. In leaq 0x18(%rax,%rbx,four), %rcx, the same address is computed, but it is not dereferenced. Instead, the computed address is moved into register %rcx.

Thanks to lea, the compiler volition also prefer the base(offset,index,scale) form over add together and mov for certain arithmetic computations on integers. For example, this teaching:

performs the function %rcx := %rax + 2 * %rbx, just in one didactics, rather than iii (movq %rax, %rcx; addq %rbx, %rcx; addq %rbx, %rcx).

%rip-relative addressing

x86-64 code frequently refers to globals using %rip-relative addressing: a global variable named a is referenced as a(%rip) rather than a.

This style of reference supports position-independent lawmaking (Flick), a security feature. Information technology specifically supports position-independent executables (PIEs), which are programs that piece of work independently of where their code is loaded into memory.

To run a conventional program, the operating arrangement loads the program'due south instructions into retentiveness at a stock-still address that's the same every time, then starts executing the program at its first instruction. This works cracking, and runs the plan in a anticipated execution environs (the addresses of functions and global variables are the same every time). Unfortunately, the very predictability of this surround makes the program easier to attack.

In a position-contained executable, the operating system loads the program at varying locations: every time information technology runs, the programme's functions and global variables have different addresses. This makes the program harder to attack (though not incommunicable).

Program startup operation matters, so the operating system doesn't recompile the program with different addresses each time. Instead, the compiler does almost of the work in advance past using relative addressing.

When the operating system loads a PIE, information technology picks a starting point and loads all instructions and globals relative to that starting point. The PIE'southward instructions never refer to global variables using direct addressing: you lot'll never see movl global_int, %eax. Globals are referenced relatively instead, using deltas relative to the next %rip: movl global_int(%rip), %eax. These relative addresses work great contained of starting point! For instance, consider an instruction located at (starting-point + 0x80) that loads a variable g located at (starting-point + 0x1000) into %rax. In a non-PIE, the instruction might exist written movq 0x400080, %rax (in compiler output, movq g, %rax); simply this relies on g having a fixed accost. In a PIE, the instruction might be written movq 0xf79(%rip), %rax (in compiler output, movq m(%rip), %rax), which works out beautifully no matter the starting point.

At starting signal…	The mov education is at…	The side by side instruction is at…	And yard is at…	So the delta (yard - next %rip) is…
0x400000	0x400080	0x400087	0x401000	0xF79
0x404000	0x404080	0x404087	0x405000	0xF79
0x4003F0	0x400470	0x400477	0x4013F0	0xF79

Arithmetics instructions

The operations of many x86-64 arithmetic instructions are easy enough to guess from their names. Then there are some arithmetic instructions, particularly those associated with Streaming SIMD Extensions and its follow-ons, that are hard to estimate (phminposuw?).

The basic arithmetic instructions on 64-bit quantities ("quadwords") are:

Educational activity	Operation	Type	Expansion
addq SRC, DST	Addition	Normal	DST := DST + SRC
subq SRC, DST	Subtraction	Normal	DST := DST - SRC
incq DST	Increment	Normal	DST := DST + i
decq DST	Decrement	Normal	DST := DST - 1
imulq SRC, DST	Signed multiplication	Normal	DST := DST * SRC
imulq SRC1, SRC2, DST	Signed multiplication	Normal	DST := SRC1 * SRC2
negq DST	Negation	Normal	DST := -DST (DST := ~DST + i)
andq SRC, DST	Bitwise and	Normal	DST := DST & SRC
orq SRC, DST	Bitwise or	Normal	DST := DST | SRC
xorq SRC, DST	Bitwise sectional or	Normal	DST := DST ^ SRC
notq DST	Complement	Normal	DST := ~DST
sal SRC, DST (also shl SRC, DST)	Left shift	Normal	DST := DST << SRC
sar SRC, DST	Signed right shift	Normal	DST := DST >> SRC, shifting in sign chip
shr SRC, DST	Unsigned correct shift	Normal	DST := DST >> SRC, shifting in zeros
cmpq SRC1, SRC2	Subtraction for flags	Flags-only	SRC2 - SRC1; meet beneath
testq SRC1, SRC2	Bitwise and for flags	Flags-just	SRC2 & SRC1; see below

At that place are as well meaty multiplication and division instructions that change multiple registers at once and take stock-still registers for some arguments. These instructions treat the combination of %rax and %rdx as a single 128-chip value where the near meaning bits (bits 64–127) of the value are stored in %rdx and the least significant bits (0–63) are stored in %rax. The division instructions compute both a caliber and a residue. (In the below, TMP is a 128-bit number.)

Instruction	Operation	Type	Expansion
imulq SRC	Signed multiplication	Mul/div	TMP := %rax * SRC; %rdx := TMP>>64; %rax := TMP
mulq SRC	Unsigned multiplication	Mul/div	TMP := %rax * SRC; %rdx := TMP>>64; %rax := TMP
idivq SRC	Signed division	Mul/div	TMP := (%rdx<<64) | %rax; %rax := TMP / SRC; %rdx := TMP % SRC
divq SRC	Unsigned division	Mul/div	TMP := (%rdx<<64) | %rax; %rax := TMP / SRC; %rdx := TMP % SRC

You may also see the adc and sbb instructions, which utilise the carry flag divers beneath.

Instruction	Operation	Blazon	Expansion
adcq SRC, DST	Addition with carry	Normal	DST := DST + SRC + CF
sbbq SRC, DST	Subtraction with infringe	Normal	DST := DST - SRC - CF

Calling convention

A calling convention governs how functions on a particular architecture and operating system interact. This includes rules about includes how function arguments are laid out, where render values get, what registers functions may use, how they may allocate local variables, then along. Calling conventions ensure that functions compiled by dissimilar compilers tin interoperate, and they ensure that operating systems tin run code from different programming languages and compilers. Some aspects of a calling convention are derived from the instruction set itself, but some are conventional, meaning decided upon by people (for instance, at a convention).

Calling conventions constrain both callers and callees. A caller is a function that calls another function; a callee is a role that was called. The currently-executing part is a callee, simply not a caller.

For concreteness, we larn the x86-64 calling conventions for Linux. These conventions are shared by many OSes, including MacOS (but non Windows), and are officially called the "System V AMD64 ABI." Run across the official specification (source).

Argument passing and stack frames

One gear up of calling convention rules governs how function arguments and return values are passed. On x86-64 Linux, the first six function arguments are passed in registers %rdi, %rsi, %rdx, %rcx, %r8, and %r9, respectively. The seventh and subsequent arguments are passed on the stack, about which more than below. The return value is passed in register %rax.

Note that floating-point values are passed in different registers. The rules hither apply to integers (including characters), pointers, and compound types comprised of integers and pointers.

The full rules more complex than this. Y'all can read them in the AMD64 ABI, department 3.2.three, but they're quite detailed. Some highlights:

1. A structure argument that fits in a unmarried automobile word (64 bits/8 bytes) is passed in a single register.

   Instance: struct small { char a1, a2; }

2. A structure that fits in 2 machine words (16–32 bytes) is passed in sequential registers, as if it were multiple arguments.

   Example: struct medium { long a1, a2; }

3. A structure that's larger than two machine words is always passed on the stack.

   Case: struct large { long a, b, c, d, e, f, yard; }

4. Floating bespeak arguments are more often than not passed in special registers, the "SSE registers," that nosotros don't hash out further.

5. Return values of up to i motorcar word are passed in %rax. Many return values that fit in two machine words—for case, a pair of longs—are passed in %rax (for the get-go eight bytes) and %rdx (for the second 8 bytes). For return values that fit merely in three or more motorcar words, the caller reserves space for the return value, and passes the address of that space every bit the kickoff statement of the role. The callee will fill in that space when it returns.

Writing footling programs to explore these rules is a pleasant exercise; for example:

                          struct              minor              {              char              a1, a2; };              int              f(small-scale south) {              return              s.a1              +              2              *              s.a2; }                      

might compile to:

                          movl              %edi,              %eax              ; copy argument to %eax                                          movsbl              %ah,              %edx              ; %edx := sign-extension of 2d byte of argument (due south.a2)                                          movsbl              %dl,              %edx              ; no-op                                          movsbl              %dil,              %eax              ; %eax := sign-extension of 1st byte of argument (south.a1)                                          leal              (%rax,%rdx,2),              %eax              ; %eax := %eax + %edx * two == s.a1 + two * due south.a2                                          ret                      

Stack

Recall that the stack is a segment of retention used to shop objects with automatic lifetime. Typical stack addresses on x86-64 expect like 0x7ffd'9f10'4f58—that is, shut to two⁴⁷.

The stack is named after a information structure, which was sort of named after pancakes. Stack data structures support at least three operations: push adds a new element to the "acme" of the stack; pop removes the elevation element, showing whatever was underneath; and superlative accesses the acme chemical element. Note what's missing: the data structure does not allow admission to elements other than the acme. (Which is sort of how stacks of pancakes piece of work.) This restriction can speed up stack implementations.

Like a stack data construction, the stack retentivity segment is only accessed from the height. The currently running function accesses its local variables; the office's caller, yard-caller, great-1000-caller, and and so forth are fallow until the currently running office returns.

x86-64 stacks await like this:

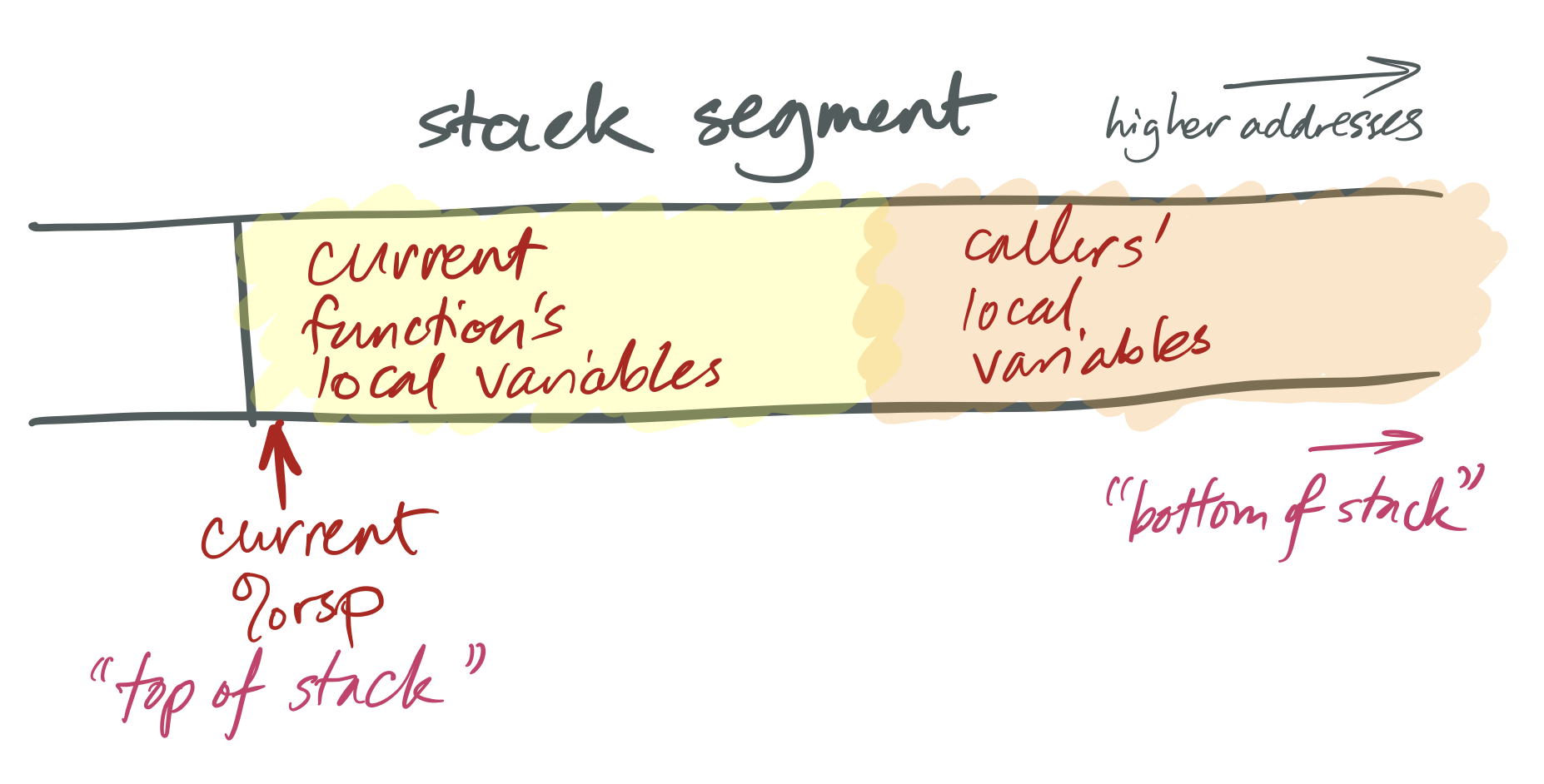
The x86-64 %rsp register is a special-purpose register that defines the current "stack arrow." This holds the address of the electric current top of the stack. On x86-64, as on many architectures, stacks grow downwardly: a "push" performance adds space for more automatic-lifetime objects past moving the stack pointer left, to a numerically-smaller address, and a "popular" operation recycles space past moving the stack arrow right, to a numerically-larger address. This ways that, considered numerically, the "top" of the stack has a smaller address than the "bottom."

This is built in to the architecture by the operation of instructions like pushq, popq, call, and ret. A push instruction pushes a value onto the stack. This both modifies the stack pointer (making it smaller) and modifies the stack segment (by moving data there). For example, the instruction pushq X means:

                          subq              $viii,              %rsp              movq              10, (%rsp)                      

And popq X undoes the outcome of pushq Ten. Information technology ways:

                          movq              (%rsp),              X              addq              $8,              %rsp                      

X can be a register or a memory reference.

The portion of the stack reserved for a office is called that function's stack frame. Stack frames are aligned: x86-64 requires that each stack frame be a multiple of xvi bytes, and when a callq instruction begins execution, the %rsp register must be 16-byte aligned. This means that every function'southward entry %rsp address will be 8 bytes off a multiple of 16.

Return address and entry and exit sequence

The steps required to call a role are sometimes called the entry sequence and the steps required to return are called the exit sequence. Both caller and callee have responsibilities in each sequence.

To prepare for a function telephone call, the caller performs the following tasks in its entry sequence.

1. The caller stores the first vi arguments in the corresponding registers.

2. If the callee takes more than than six arguments, or if some of its arguments are large, the caller must store the surplus arguments on its stack frame. It stores these in increasing order, so that the seventh argument has a smaller address than the 8th argument, and and then along. The 7th argument must exist stored at (%rsp) (that is, the tiptop of the stack) when the caller executes its callq instruction.

3. The caller saves any caller-saved registers (see below).

4. The caller executes callq FUNCTION. This has an effect like pushq $NEXT_INSTRUCTION; jmp Office (or, equivalently, subq $eight, %rsp; movq $NEXT_INSTRUCTION, (%rsp); jmp FUNCTION), where NEXT_INSTRUCTION is the address of the teaching immediately following callq.

This leaves a stack like this:

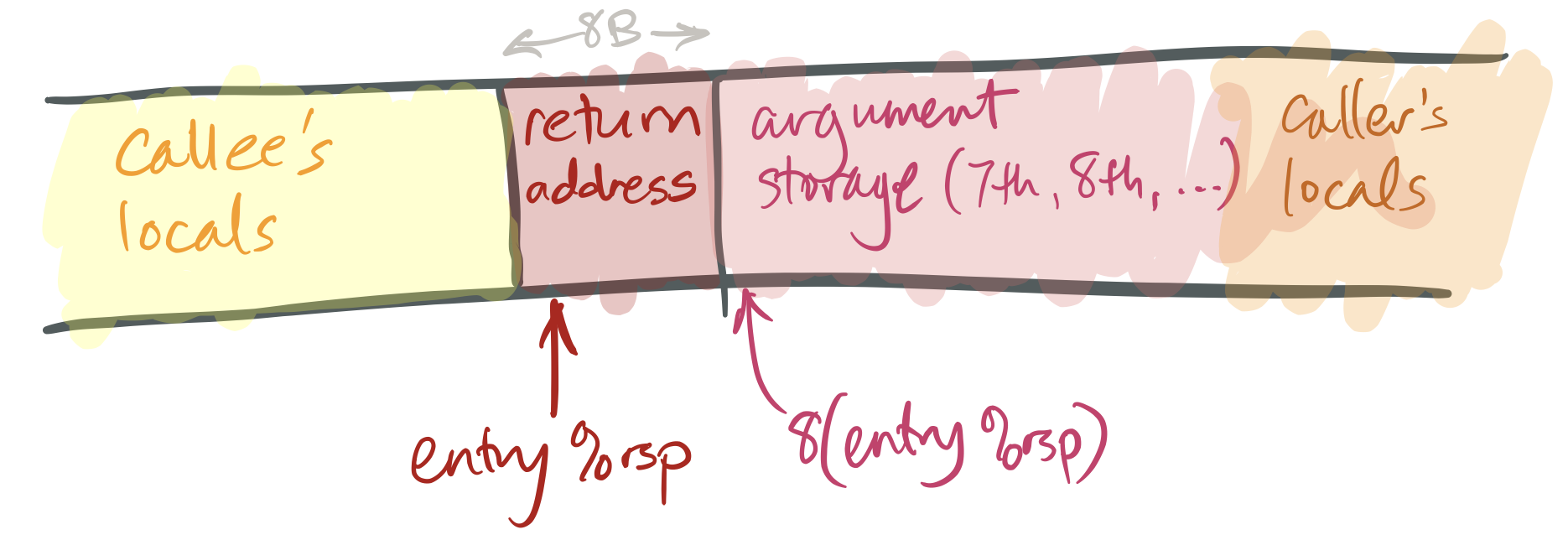
To return from a role:

1. The callee places its return value in %rax.

2. The callee restores the stack pointer to its value at entry ("entry %rsp"), if necessary.

3. The callee executes the retq instruction. This has an effect like popq %rip, which removes the return address from the stack and jumps to that accost.

4. The caller then cleans up any space it prepared for arguments and restores caller-saved registers if necessary.

Particularly uncomplicated callees don't demand to do much more than than return, but most callees will perform more than tasks, such as allocating space for local variables and calling functions themselves.

Callee-saved registers and caller-saved registers

The calling convention gives callers and callees certain guarantees and responsibilities virtually the values of registers across role calls. Office implementations may expect these guarantees to hold, and must work to fulfill their responsibilities.

The near important responsibility is that certain registers' values must be preserved across function calls. A callee may use these registers, but if it changes them, it must restore them to their original values before returning. These registers are called callee-saved registers. All other registers are caller-saved.

Callers can simply use callee-saved registers across part calls; in this sense they deport like C++ local variables. Caller-saved registers behave differently: if a caller wants to preserve the value of a caller-saved register beyond a role call, the caller must explicitly save it before the callq and restore it when the function resumes.

On x86-64 Linux, %rbp, %rbx, %r12, %r13, %r14, and %r15 are callee-saved, as (sort of) are %rsp and %rip. The other registers are caller-saved.

Base pointer (frame pointer)

The %rbp register is called the base arrow (and sometimes the frame pointer). For uncomplicated functions, an optimizing compiler generally treats this like whatsoever other callee-saved general-purpose register. However, for more complex functions, %rbp is used in a specific pattern that facilitates debugging. It works like this:

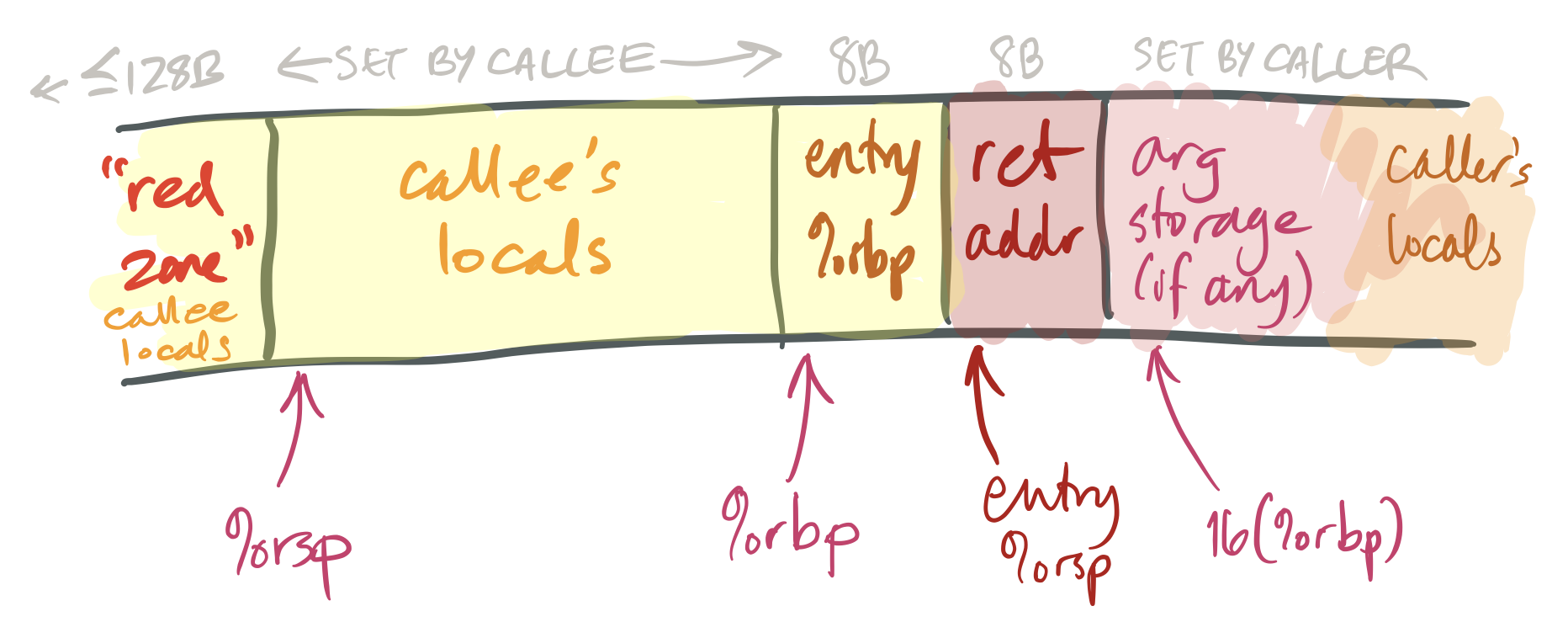
1. The get-go pedagogy executed on function entry is pushq %rbp. This saves the caller's value for %rbp into the callee'southward stack. (Since %rbp is callee-saved, the callee must salvage it.)

2. The second pedagogy is movq %rsp, %rbp. This saves the electric current stack pointer in %rbp (so %rbp = entry %rsp - 8).

   This adjusted value of %rbp is the callee's "frame pointer." The callee will not change this value until information technology returns. The frame pointer provides a stable reference signal for local variables and caller arguments. (Complex functions may need a stable reference signal because they reserve varying amounts of space for calling different functions.)

   Note, also, that the value stored at (%rbp) is the caller's %rbp, and the value stored at eight(%rbp) is the return address. This information can be used to trace backwards through callers' stack frames by functions such as debuggers.

3. The function ends with movq %rbp, %rsp; popq %rbp; retq, or, equivalently, get out; retq. This sequence restores the caller's %rbp and entry %rsp before returning.

Stack size and red zone

Functions execute fast considering allocating space within a office is simply a affair of decrementing %rsp. This is much cheaper than a call to malloc or new! But making this piece of work takes a lot of machinery. We'll encounter this in more particular subsequently; simply in brief: The operating system knows that %rsp points to the stack, so if a function accesses nonexistent memory near %rsp, the Os assumes it'due south for the stack and transparently allocates new retentiveness there.

And so how can a program "run out of stack"? The operating system puts a limit on each function's stack, and if %rsp gets likewise low, the programme segmentation faults.

The diagram above too shows a squeamish feature of the x86-64 architecture, namely the ruby zone. This is a small expanse above the stack arrow (that is, at lower addresses than %rsp) that can exist used by the currently-running function for local variables. The crimson zone is nice because information technology tin be used without mucking around with the stack pointer; for small-scale functions button and pop instructions end up taking time.

Branches

The processor typically executes instructions in sequence, incrementing %rip each time. Deviations from sequential instruction execution, such as part calls, are called control menstruation transfers.

Function calls aren't the only kind of command menses transfer. A branch instruction jumps to a new instruction without saving a return accost on the stack.

Branches come in two flavors, unconditional and conditional. The jmp or j instruction executes an unconditional branch (like a goto). All other branch instructions are conditional: they only branch if some condition holds. That condition is represented past status flags that are set as a side effect of every arithmetic operation.

Arithmetic instructions change office of the %rflags register as a side effect of their functioning. The nearly often used flags are:

• ZF (zero flag): prepare iff the result was zero.
• SF (sign flag): ready iff the most significant bit (the sign bit) of the consequence was ane (i.east., the effect was negative if considered as a signed integer).
• CF (carry flag): set iff the result overflowed when considered as unsigned (i.eastward., the issue was greater than 2^Westward-1).
• OF (overflow flag): ready iff the issue overflowed when considered as signed (i.due east., the result was greater than 2^W-one-1 or less than –2^W-1).

Flags are almost often accessed via conditional jump or provisional move instructions. The provisional branch instructions are:

Teaching	Mnemonic	C case	Flags
j (jmp)	Leap	break;	(Unconditional)
je (jz)	Jump if equal (aught)	if (10 == y)	ZF
jne (jnz)	Jump if non equal (nonzero)	if (x != y)	!ZF
jg (jnle)	Jump if greater	if (ten > y), signed	!ZF && (SF == OF)
jge (jnl)	Jump if greater or equal	if (x >= y), signed	SF == OF
jl (jnge)	Bound if less	if (x < y), signed	SF != OF
jle (jng)	Jump if less or equal	if (ten <= y), signed	ZF || (SF != OF)
ja (jnbe)	Jump if above	if (ten > y), unsigned	!ZF && !CF
jae (jnb)	Leap if to a higher place or equal	if (x >= y), unsigned	!CF
jb (jnae)	Jump if below	if (10 < y), unsigned	CF
jbe (jna)	Jump if below or equal	if (x <= y), unsigned	ZF || CF
js	Jump if sign bit	if (x < 0), signed	SF
jns	Bound if not sign bit	if (x >= 0), signed	!SF
jc	Jump if carry bit	N/A	CF
jnc	Jump if not carry fleck	N/A	!CF
jo	Jump if overflow fleck	N/A	OF
jno	Jump if not overflow flake	N/A	!OF

The test and cmp instructions are frequently seen before a conditional branch. These operations perform arithmetic but throw away the result, except for condition codes. test performs binary-and, cmp performs subtraction.

cmp is hard to grasp: retrieve that subq %rax, %rbx performs %rbx := %rbx - %rax—the source/destination operand is on the left. And then cmpq %rax, %rbx evaluates %rbx - %rax. The sequence cmpq %rax, %rbx; jg 50 will jump to label 50 if and only if %rbx is greater than %rax (signed).

The weird-looking instruction testq %rax, %rax, or more mostly testq REG, SAMEREG, is used to load the condition flags appropriately for a single register. For case, the bitwise-and of %rax and %rax is zero if and but if %rax is zero, so testq %rax, %rax; je Fifty jumps to L if and only if %rax is zero.

You volition besides see instructions named setFLAG that load the binary value of a condition (0 or 1) into an 8-fleck register. For example, setz %al sets %al to 1 if the zero flag ZF is on, and 0 otherwise. There are set up constructions for all conditions. set up instructions are oftentimes followed by goose egg-extending instructions: setz %al; movzbl %al, %eax sets all of %rax to one if the aught flag ZF is on, and 0 otherwise.

Instruction	Mnemonic	Expansion
sete DST (setz DST)	Load equal (aught flag)	DST := ZF
setne DST (setnz DST)	Load not equal (flipped zero flag)	DST := !ZF
setg DST (setnle DST)	Load greater, signed	DST := !ZF && (SF == OF)
setge DST (setnl DST)	Load greater or equal, signed	DST := (SF == OF)
setl DST (setnge DST)	Load less, signed	DST := (SF != OF)
setle DST (setng DST)	Load less or equal, signed	DST := ZF || (SF != OF)
seta DST (setnbe DST)	Load above, unsigned	DST := (!ZF && !CF)
setae DST (setnb DST)	Load to a higher place or equal, unsigned	DST := !CF
setb DST (setnae DST)	Load below, unsigned	DST := CF
setbe DST (setna DST)	Load beneath or equal, unsigned	DST := (ZF || CF)
sets DST	Load sign flag	DST := SF
setns DST	Load flipped sign flag	DST := !SF
setc DST	Load comport flag	DST := CF
setnc DST	Load flipped conduct flag	DST := !CF
seto DST	Load overflow flag	DST := OF
setno DST	Load flipped overflow flag	DST := !OF

Data-motion and control-flow instructions practise not change flags. Oddly, for case, lea does not alter flags (it counts as data movement), though add does (it counts every bit arithmetic).

Sidebar: C++ data structures

C++ compilers and data construction implementations accept been designed to avoid the then-called abstraction penalty, which is when convenient information structures compile to more than and more-expensive instructions than simple, raw retentivity accesses. When this works, information technology works quite well; for instance, this:

                          long              f(std::vector<              int              >&              v) {              long              sum              =              0;              for              (car              &              i              : five) {         sum              +=              i;     }              return              sum; }                      

compiles to this, a very tight loop similar to the C version:

                          movq              (%rdi),              %rax              movq              viii(%rdi),              %rcx              cmpq              %rcx,              %rax              je              .L4              movq              %rax,              %rdx              addq              $4,              %rax              subq              %rax,              %rcx              andq              $-4,              %rcx              addq              %rax,              %rcx              movl              $0,              %eax              .L3:              movslq              (%rdx),              %rsi              addq              %rsi,              %rax              addq              $4,              %rdx              cmpq              %rcx,              %rdx              jne              .L3              rep              ret              .L4:              movl              $0,              %eax              ret                      

This output also confirms some of our earlier observations near std::vector's implementation:

• The first element of a std::vector structure seems to be a arrow to the first element of the vector;
• The elements are stored in retentivity in a unproblematic array;
• The second element of a std::vector structure is a pointer to 1-past-the-finish of the elements of the vector (i.e., if the vector is empty, the first and second elements of the structure have the same value).

Compiler optimizations

Argument elision

A compiler may decide to elide (or remove) sure operations setting upwards function telephone call arguments, if it tin decide that the registers containing these arguments will agree the correct value before the part call takes identify. Permit's see an example of a function disassembled function f in f31.s:

                          subq              $8,              %rsp              call              _Z1gi@PLT              addq              $8,              %rsp              addl              $1,              %eax              ret                      

This function calls another part g, adds i to g's return value, and returns that value.

It is possible that the function has the following definition in C++:

                          int              f() {              render              1              +              g(); }                      

However, the actual definition of f in f31.cc is:

                          int              f(x) {              render              1              +              g(x); }                      

The compiler realizes that the statement to role g, which is passed via annals %rdi, already has the right value when thousand is called, and so it doesn't bother doing annihilation almost it. This is one example of numerous optimizations a compiler can perform to reduce the size of generated code.

Inlining

A compiler may also re-create the body of function to its call site, instead of doing an explicit function call, when information technology decides that the overhead of performing a function call outweights the overhead of doing this re-create. For example, if nosotros have a role 1000 defined equally g(x) = 2 + x, and f is defined as f(x) = i + grand(10), then the compiler may actually generate f(x) every bit simply iii + x, without inserting any call instructions. In assembly terms, function g will look like

and f will just exist

Tail telephone call emptying

Let's look at some other example in f32.s:

                          addl              $one,              %edi              jmp              _Z1gi@PLT                      

This function doesn't fifty-fifty contain a ret education! What is going on? Let's take a look at the actual definition of f, in f32.cc:

                          int              f(int              x) {              return              grand(10              +              ane); }                      

Notation that the call to role g is the concluding performance in function f, and the return value of f is just the render value of the invocation of one thousand. In this case the compiler tin perform a tail telephone call elimination: instead of calling g explicitly, it can simply jump to g and have g return to the same address that f would accept returned to.

A tail telephone call emptying may occur if a function (caller) ends with another role call (callee) and performs no cleanup one time the callee returns. In this case the caller and simply jump to the callee, instead of doing an explicit call.

Loop unrolling

Before nosotros jump into loop unrolling, let'south accept a pocket-sized excursion into an aspect of calling conventions called caller/callee-saved registers. This will help us under the sample plan in f33.south improve.

Calling conventions: caller/callee-saved registers

Permit's look at the function definition in f33.s:

                          pushq              %r12              pushq              %rbp              pushq              %rbx              testl              %edi,              %edi              je              .L4              movl              %edi,              %r12d              movl              $0,              %ebx              movl              $0,              %ebp              .L3:              movl              %ebx,              %edi              call              _Z1gj@PLT              addl              %eax,              %ebp              addl              $1,              %ebx              cmpl              %ebx,              %r12d              jne              .L3              .L1:              movl              %ebp,              %eax              popq              %rbx              popq              %rbp              popq              %r12              ret              .L4:              movl              %edi,              %ebp              jmp              .L1                      

From the assembly we can tell that the backwards jump to .L3 is likely a loop. The loop index is in %ebx and the loop bound is in %r12d. Note that upon entry to the office we first moved the value %rdi to %r12d. This is necessary considering in the loop f calls g, and %rdi is used to pass arguments to g, so we must move its value to a unlike register to used it every bit the loop leap (this case %r12). Simply there is more to this: the compiler as well needs to ensure that this annals'southward value is preserved beyond office calls. Calling conventions dictate that certain registers e'er showroom this property, and they are called callee-saved registers. If a register is callee-saved, then the caller doesn't accept to save its value before entering a part call.

We annotation that upon entry to the function, f saved a bunch of registers by pushing them to the stack: %r12, %rbp, %rbx. Information technology is because all these registers are callee-saved registers, and f uses them during the function telephone call. In general, the post-obit registers in x86_64 are callee-saved:
%rbx, %r12-%r15, %rbp, %rsp (%rip)

All the other registers are caller-saved, which means the callee doesn't have to preserve their values. If the caller wants to reuse values in these registers beyond office calls, information technology will have to explicitly salvage and restore these registers. In general, the following registers in x86_64 are caller-saved:
%rax, %rcx, %rdx, %r8-%r11

Now permit's go back to loop unrolling. Let u.s. a look at the program in f34.s:

                          testl              %edi,              %edi              je              .L7              leal              -1(%rdi),              %eax              cmpl              $7,              %eax              jbe              .L8              pxor              %xmm0,              %xmm0              movl              %edi,              %edx              xorl              %eax,              %eax              movdqa              .LC0(%rip),              %xmm1              shrl              $2,              %edx              movdqa              .LC1(%rip),              %xmm2              .L5:              addl              $1,              %eax              paddd              %xmm1,              %xmm0              paddd              %xmm2,              %xmm1              cmpl              %edx,              %eax              jb              .L5              movdqa              %xmm0,              %xmm1              movl              %edi,              %edx              andl              $-4,              %edx              psrldq              $8,              %xmm1              paddd              %xmm1,              %xmm0              movdqa              %xmm0,              %xmm1              cmpl              %edx,              %edi              psrldq              $4,              %xmm1              paddd              %xmm1,              %xmm0              movd              %xmm0,              %eax              je              .L10              .L3:              leal              i(%rdx),              %ecx              addl              %edx,              %eax              cmpl              %ecx,              %edi              je              .L1              addl              %ecx,              %eax              leal              ii(%rdx),              %ecx              cmpl              %ecx,              %edi              je              .L1              addl              %ecx,              %eax              leal              iii(%rdx),              %ecx              cmpl              %ecx,              %edi              je              .L1              addl              %ecx,              %eax              leal              iv(%rdx),              %ecx              cmpl              %ecx,              %edi              je              .L1              addl              %ecx,              %eax              leal              5(%rdx),              %ecx              cmpl              %ecx,              %edi              je              .L1              addl              %ecx,              %eax              leal              6(%rdx),              %ecx              cmpl              %ecx,              %edi              je              .L1              addl              %ecx,              %eax              addl              $7,              %edx              leal              (%rax,%rdx),              %ecx              cmpl              %edx,              %edi              cmovne              %ecx,              %eax              ret              .L7:              xorl              %eax,              %eax              .L1:              rep              ret              .L10:              rep              ret              .L8:              xorl              %edx,              %edx              xorl              %eax,              %eax              jmp              .L3                      

Wow this looks long and repetitive! Especially the department under label .L3! If we take a look at the original function definition in f34.cc, we volition find that it's almost the same as f33.cc, except that in f34.cc we know the definition of thousand besides. With cognition of what g does the compiler'south optimizer decides that unrolling the loop into seven-increment batches results in faster lawmaking.

Lawmaking like this tin go difficult to empathise, especially when the compiler begins to use more advanced registers reserved for vector operations. We can fine-tune the optimizer to disable certain optimizations. For example, we tin utilize the -mno-sse -fno-unroll-loops compiler options to disable the use of SSE registers and loop unrolling. The resulting code, in f35.s, for the aforementioned role definitions in f34.cc, becomes much easier to understand:

                          testl              %edi,              %edi              je              .L4              xorl              %edx,              %edx              xorl              %eax,              %eax              .L3:              addl              %edx,              %eax              addl              $1,              %edx              cmpl              %edx,              %edi              jne              .L3              rep              ret              .L4:              xorl              %eax,              %eax              ret                      

Notation that the compiler still performed inlining to eliminate role thou.

Optimizing recursive functions

Let'southward look at the following recursive part in f36.cc:

                          int              f(int              x) {              if              (10              >              0) {              render              10              *              f(x              -              ane);     }              else              {              return              0;     } }                      

At the first glance it may seem that the role returns factorial of 10. But it actually returns 0. Despite it doing a serial of multiplications, in the end it ever multiplies the whole result with 0, which produces 0.

When nosotros compile this function to assembly without much optimization, we see the expensive computation occurring:

                          movl              $0,              %eax              testl              %edi,              %edi              jg              .L8              rep              ret              .L8:              pushq              %rbx              movl              %edi,              %ebx              leal              -1(%rdi),              %edi              call              _Z1fi              imull              %ebx,              %eax              popq              %rbx              ret                      

In f37.cc in that location is an actual factorial part:

                          int              f(int              x) {              if              (x              >              0) {              return              ten              *              f(x              -              1);     }              else              {              render              1;     } }                      

If nosotros compile this function using level-2 optimization (-O2), we get the following assembly:

                          testl              %edi,              %edi              movl              $ane,              %eax              jle              .L4              .L3:              imull              %edi,              %eax              subl              $i,              %edi              jne              .L3              rep              ret              .L4:              rep              ret                      

There is no telephone call instructions once more! The compiler has transformed the recursive function into a loop.

If nosotros revisit our "fake" factorial function that e'er returns 0, and compile it with -O2, we see yet more evidence of compiler's deep understanding of our programme:

Optimizing arithmetics operations

The assembly code in f39.due south looks like this:

                          leal              (%rdi,%rdi,2),              %eax              leal              (%rdi,%rax,4),              %eax              ret                      

Information technology looks like some rather complex address computations! The kickoff leal educational activity basically loads %eax with value 3*%rdi (or %rdi + 2*%rdi). The second leal multiplies the previous result past another 4, and adds another %rdi to information technology. So what it actually does is iii*%rdi*4 + %rdi, or only 13*%rdi. This is also revealed in the role name in f39.s.

The compiler choose to apply leal instructions instead of an explicit multiply because the two leal instructions actually take less space.

Source: https://cs61.seas.harvard.edu/site/2021/Asm/

Posted by: demelobunecand.blogspot.com

Share this post